20210130 图灵杯

G 贪吃的派蒙
题目描述
在遥远的提瓦特大陆上，正在筹备一年一度的羽球节，猎鹿人餐厅为犒劳认真筹备的众人，准备了 K 份甜甜花酿鸡供大家排队领取。
在每一次的排队中，编号为 i 的角色领取上限为 Ai，这意味着他可以领取的甜甜花酿鸡在[1-Ai] 范围内。当一个角色领完本次的甜甜花酿鸡，他/她就会回到队列的末尾，直到所有甜甜花酿鸡都被吃完为止。当轮到一个角色领取时，如果所有的甜甜花酿鸡都被领完，那么他/她就要帮大家刷盘子。
贪吃的派蒙每次都吃固定的 Ax 个甜甜花酿鸡 (如果剩下的甜甜花酿鸡的数量比 Ax 小，那么他就把剩下的都吃完)。我们很容易找到派蒙的编号，Ax 比其他所有的 Ai 都要大。大家都想让派蒙最后留下来刷盘子，请你写一个程序来判断这是否可能。
输入描述:
第一行包含一个整数 T(1≤T≤100)，表示有 T 组测试数据。
接下来每组测试数据包含两行。
第一行包含两个整数 N 和 K(2≤N≤10^5
0≤K≤10^8)，分别表示人数和甜甜花酿鸡的数量。
第二行包含一个整数 Ai(1≤Ai≤10^9)，表示队列中编号为 i 的角色可以领取甜甜花酿鸡的最大数量。始终只有一个最大的 Ax。
输出描述:
如果大家能找到一种方案让派蒙刷盘子，那么输出“YES”。否则输出“NO”。
示例 1
输入：
1
4 3
1 2 3 2
输出：
YES
示例 2
输入：
1
5 8
1 2 3 2 1
输出：
NO
分析
根据题意，此题需要先后解决两个问题：（1）派蒙的位置。（2）什么情况下派蒙刚好吃不到甜甜花酿鸡。派蒙的位置很容易确定，通过遍历一次数组，找到最大元素的位置即确定派蒙的位置。那怎么判断在 K 个甜甜花酿鸡情况下，派蒙是否刚好吃不到甜甜花酿鸡？
我们可以从小量甜甜花酿鸡开始分析：题意表明，除派蒙外，每个人至少吃 1 个，我们假定派蒙的位置为 pos，如果甜甜花酿鸡数量小于 pos-1即还没到派蒙，甜甜花酿鸡就吃完了，此情况下，派蒙一定不会刷盘子，派蒙之前的人一定会刷盘子。我们知道每个人最多吃 Ai 个，如果甜甜花酿鸡数量略微大于 pos 之前 Ai 之和，那派蒙一定不会刷盘子，派蒙之后的人一定会刷盘子。（注意：此处情况是略微大于，一会我们将讨论远大于的情况）。也就是说甜甜花酿鸡数量在 pos-1 到 pre_sum[pos-1] 闭区间派蒙一定会刷盘子。现在我们分析甜甜花酿鸡数量很大的情况，我们可以这么想：经过 rounds 轮后，剩余的甜甜花酿鸡数量已经不够下一轮了，此时情况与小量情况一模一样。至此，此题基本就解决了。
现在有一个重要问题没有解决：每轮中，整个队的人吃多少个甜甜花酿鸡？我们可以假定整个队的人每次吃个特殊数，即极大数或者极小数。因为只有这样我们才能得到更多的信息来分析。一个队吃的最小值为 min_sum，最大值为：max_sum。我们假定一个队吃最小值，这样可以得到一个重要信息：K 个甜甜花酿鸡最多 rounds 轮后就吃完了。同时我们将剩下 left 个。现在我们判断 left。若 left 比 pos-1 小，也就是上一轮多吃了，因为每次只吃最小，所以我们只需 left 加 min_sum（也就是说多吃了一轮）。同时，rounds 减一，然后再判断 left。若 left 比 pre_sum[pos-1] 大，也就是说在 rounds 轮中吃少了，我们需要将多出部分分到 rounds 轮中。怎么将多出部分分到 rounds 轮中？具体分法我们可以不用管，但是我们发现，若 left - pre_sum[pos-1] 大于 rounds*(max_sum - min_sum)，即之前都吃最大时，仍有剩余，则派蒙一定不会刷盘子。
具体实现代码如下：
#include<algorithm>
#include<vector>
#include<stack>
#include<unordered_map>
#include<iostream>
#include<unordered_set>
#include<cstring>
#include<set>
#include<map>
#include<queue>
#include<ctype.h>
#define MAX 111111
const int MOD = 1e9;
using namespace std;
typedef long long int ll;
ll arr[MAX];
ll pre_sum[MAX];
ll left_low;
ll left_high;
int n,k,t,pos;
void print();
int main(void)
{
int i;
cin >> t;
while(t--)
{
pos = 1;
cin >> n >> k;
for(i=1; i<=n; ++i)
{
cin >> arr[i];
if(arr[i] > arr[pos])
pos = i;
pre_sum[i] = arr[i] + pre_sum[i-1];
}
left_low = pos-1; //派蒙刷盘子的最小值
left_high = pre_sum[pos-1]; //派蒙刷盘子的最大值
print();
}
return 0;
}
void print()
{
ll min_sum = n-1+arr[pos]; //该队能吃的最小值
ll max_sum = pre_sum[n]; //该队能吃的最大值
ll rounds = k/min_sum; //最多 rounds 轮
ll left = k%min_sum; //剩余量
ll temp = 0;
ll max_minus = 0;
while(1) //循环判断每一次 left
{
if(left>= left_low && left<= left_high)
{
printf("YES\n");
return;
}
if(left > left_high)
{
temp = left - left_high;
max_minus = rounds*(max_sum - min_sum);//之前均吃最大
if(temp > max_minus) // 若之前均吃最大值后，仍有剩余
{
printf("NO\n");
return;
}
}
if(left < left_low)
{
if(!rounds) //若 rounds 为零，left 仍小于 left_low
{
printf("NO\n");
return;
}
left += min_sum;
--rounds;
}
}
return;

int main() {
int k;
cin >> k;
cout << k + 2047 << endl;
for (int i = 0; i < 11; i++)
for (int j = 1; j <= (1<<i); j++)
cout << 1 << ' ' << i << endl;
int x = (1<<11) / k;
for (int i = 1; i <= k; i++) {
cout << 2 << ' ' << x << ' ';
for (int j = 1; j <= x; j++) cout << "11 ";
cout << endl;
}
return 0;
}
2|0B 小宝的幸运数组

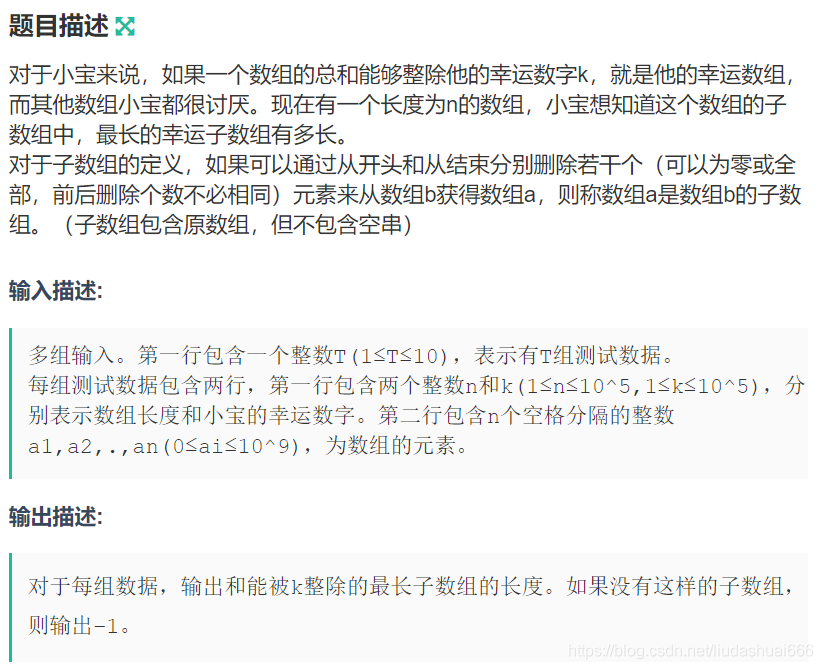
就是要求能被 k 整除的最大连续子数组的长度嘛。数据范围这么大，暴力必 TLE。可以先用 sum[] 去记录前 i 项的和。假设前 m 项的和取模 k 得到 x, 前 n 项的和取模 k 得到的也是 x, 那么 m+1-n 这个子序列的和肯定是能够被 k 整除的。想到这个那么问题就很简单了。
2|1Code：

ll a[100005], sum[100005];
ll pos[100005];
int main() {
int t;
cin >> t;
while (t--) {
int n, k;
cin >> n >> k;
for (int i = 1; i <= n; i++) {
cin >> a[i];
sum[i] = sum[i-1] + a[i];
}
mem(pos, INF);
ll ans = -1;
for (int i = 1; i <= n; i++) {
ll m = sum[i] % k;
if (m == 0) ans = max(ans, 1ll*i);
if (pos[m] != INF) ans = max(ans, i - pos[m]);
pos[m] = min(pos[m], 1ll*i);
}
cout << ans << endl;
}

return 0;
}

|0E Seek the Joker II

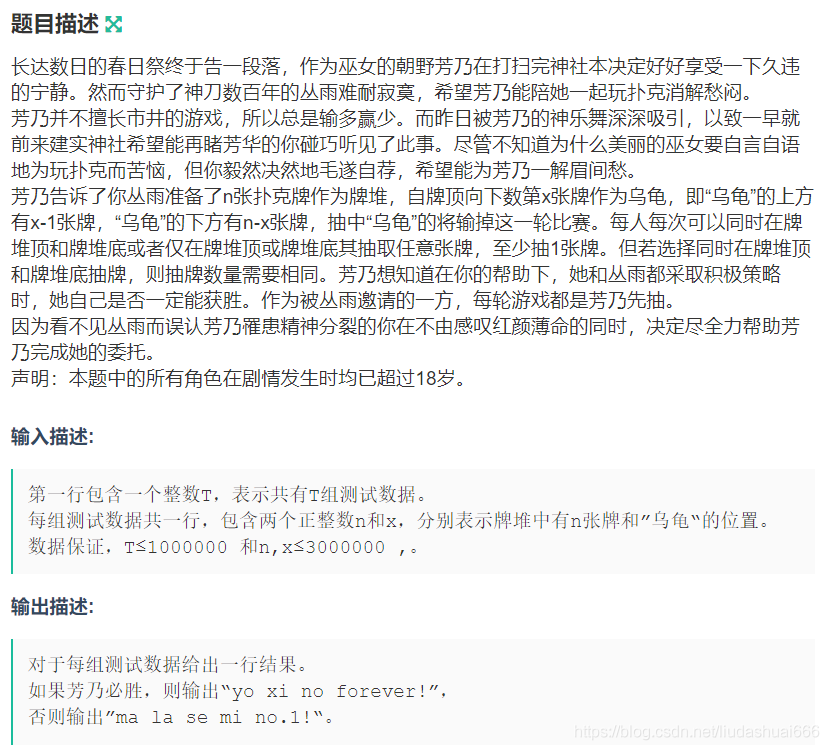
两堆石子，一堆 k-1，另一堆 n-k，先取到任意一堆的最后一个输，emm，这不是威佐夫博弈嘛。啪的一下就 AC 了，很快啊~
5|1Code：

const double GSR=(1+sqrt(5.0))/2;
int main() {
int t;
cin >> t;
while (t--) {
int n, k;
cin >> n >> k;
int a = k-1, b = n-k;
if(a > b) swap(a, b);
if(a == (int)(GSR*(b-a)))
cout << "ma la se mi no.1!" << endl;
else
cout << "yo xi no forever!" << endl;
}
return 0;
}
6|0F 成绩查询 ing

交了一发暴力，先 TLE 为敬。然后就掏出了 C with STL 的传统艺能 map+set，想着应该能过，结果还是 TLE 了，补题的时候才发现。。。把 endl 改成 "\n" 直接就能过，emm，这又是什么玄学，然后听说endl 要比 "\n" 慢一些，然后嘛。。。反手就加了一句
#define endl “\n”
（毕竟疯起来连 int 都 define 成 longlong~~手动狗头~~）
6|1Code：

struct node {
string name;
int grade, sex, sno;
}s[100005];
int cmp(node a, node b) {
return a.name<b.name;
}
map<string, node> m;
set<string> se[200];
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++)
cin >> s[i].name >> s[i].grade >> s[i].sex >> s[i].sno;
sort(s, s+n, cmp);
for (int i = 0; i < n; i++) {
m[s[i].name] = s[i];
se[s[i].grade].insert(s[i].name);
}
int t;
cin >> t;
while (t--) {
int op;
cin >> op;
if (op == 1) {
string str;
cin >> str;
node tmp = m[str];
if (tmp.sno != 0) {
cout << tmp.grade << ' ' << tmp.sno << ' ' << tmp.sex <<endl;
}
} else {
int grade;
cin >> grade;
set<string>::iterator it;
it = se[grade].begin();
for(;it!=se[grade].end();it++)
cout<<*it<<endl;
}
}
return 0;
}

L 建立火车站

12|0L 建立火车站
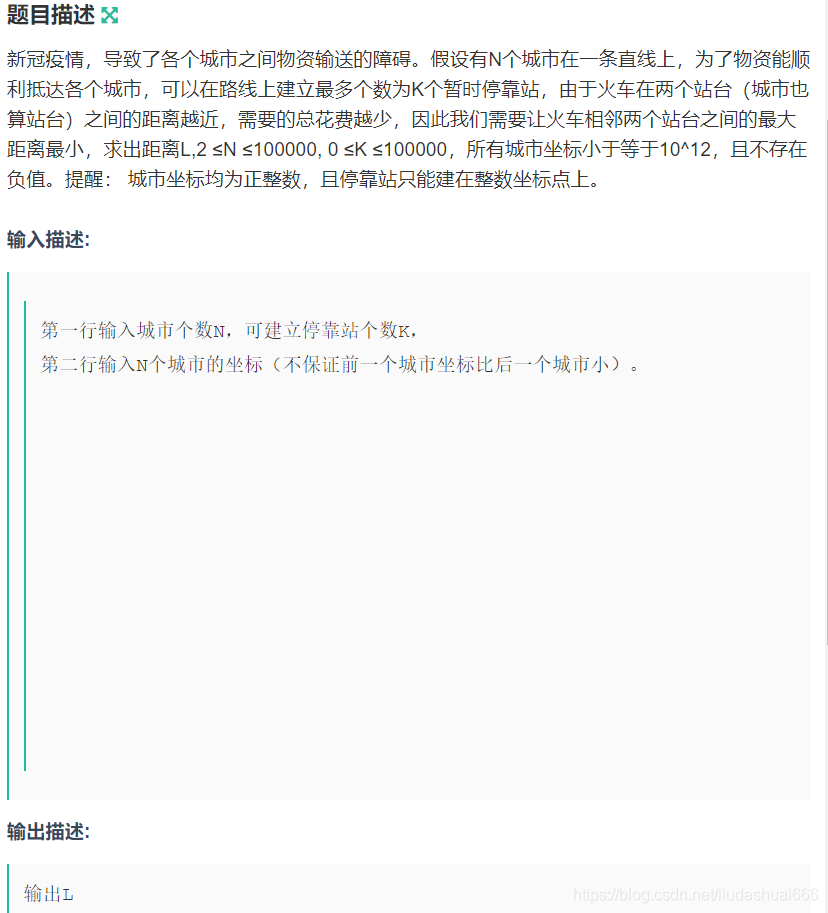
![image5](/img/user/resources/attachments/image5-5 1.png)
先用节点存城市与城市之间的距离（sum）、被分成段的长度（val）以及它们之间站台数 +1（len）。然后拿优先队列存节点，按 val 降序排列。循环 k 次每次取 val 最大的，并弹出节点，len++，更新 val（val=sum/len），再把新的节点 push 进去，最后队顶的 val 就是答案（当然啦，如果最后的 val 是小数，那么结果应该是 val 的整数部分 +1）。
12|1Code：

struct node {
friend bool operator< (node a, node b) {
return a.val < b.val;
}
ll len;
long double val, sum;
};
priority_queue<node> q;
ll dt[100005], a[100005];
int main() {
int n, k;
cin >> n >> k;
for (int i = 0; i < n; i++) {
cin >> a[i];
}
sort(a, a+n);
for (int i = 1; i < n; i++)
dt[i] = a[i]-a[i-1];
for (int i = 1; i < n; i++) {
node tmp;
tmp.val = tmp.sum = dt[i];
tmp.len = 1;
q.push(tmp);
}
while (k--) {
node tmp = q.top();
q.pop();
tmp.len++;
tmp.val = tmp.sum/tmp.len;
q.push(tmp);
}
node ans = q.top();
ll key = (ll)ans.val;
if (ans.val == key) cout << key << endl;
else cout << key+1 << endl;
return 0;
}